Stable Matching

Definition

Goal: Given n men and n women, find a "suitable" matching.

• Participants rate members of opposite sex.
• Each man lists women in order of preference from best to worst.
• Each woman lists men in order of preference from best to worst.

特征：二分图，按照优先度排序

Unstable pair: applicant x and hospital y are unstable if:

• x prefers y to its assigned hospital
• y prefers x to one of its admitted students.

Stable assignment: Assignment with no unstable pairs.

• Natural and desirable condition.
• Individual self-interest will prevent any applicant/hospital deal from being made.

Perfect matching: everyone is matched monogamously

• Each man gets exactly one woman.
• Each woman gets exactly one man.

Stability：no incentive for some pair of participants to undermine assignment by joint action。

• In matching M, an unmatched pair m-w is unstable if man m and woman w prefer each other to current partners.
• Unstable pair m-w could each improve by eloping.

Stable matching：perfect matching with no unstable pairs.

Stable matching problem: Given the preference lists of n men and n women, find a stable matching if one exists.

稳定匹配不一定存在，如分配室友：

Stable roommate problem：

• 2n people; each person ranks others from 1 to 2n-1.
• Assign roommate pairs so that no unstable pairs.

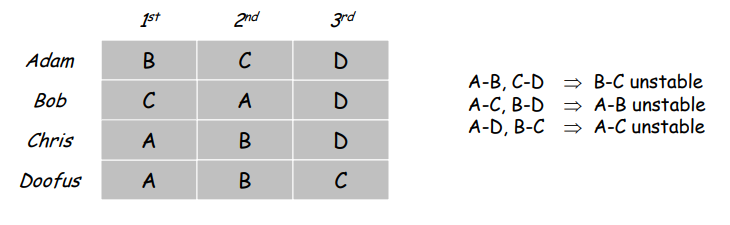
此反例可以结合二分图中的相关证明理解

Gale-Shapley Algorithm

Initialize each person to be free.
while (some man is free and hasn't proposed to every woman) {
	Choose such a man m
 		w = 1st woman on m's list to whom m has not yet proposed
 	if (w is free)
 		assign m and w to be engaged
 	else if (w prefers m to her fiancé m')
 		assign m and w to be engaged, and m' to be free
 	else
 	w rejects m
}

Proof of Correctness

Termination

Observation:

• Men propose to women in decreasing order of preference
• Once a woman is matched, she never becomes unmatched; she only "trades up."

Claim: Algorithm terminates after at most $n^2$ iterations of while loop.

Each time through the while loop a man proposes to a new woman. There are only n2 possible proposals.

Perfection

Claim. All men and women get matched.

Pf. (by contradiction)

• Suppose, for sake of contradiction, that Zeus is not matched upontermination of algorithm.
• Then some woman, say Amy, is not matched upon termination.
• By Observation 2, Amy was never proposed to.
• But, Zeus proposes to everyone, since he ends up unmatched. ▪

Stability

Claim. No unstable pairs.

Pf. (by contradiction)

• Suppose A-Z is an unstable pair: each prefers each other topartner in Gale-Shapley matching S*.
• Case 1: Z never proposed to A.
• Z prefers his GS partner to A.
• A-Z is stable.
• Case 2: Z proposed to A.
• A rejected Z (right away or later)
• A prefers her GS partner to Z.
• A-Z is stable.
• In either case A-Z is stable, a contradiction. ▪

Efficient Implementation

Representing men and women：

• Assume men are named 1, …, n.
• Assume women are named 1', …, n'.

Engagements：

• Maintain a list of free men, e.g., in a queue
• Maintain two arrays wife[m], and husband[w].
• set entry to 0 if unmatched
• if m matched to w then wife[m]=w and husband[w]=m

Men proposing:

• For each man, maintain a list of women, ordered by preference
• Maintain an array count[m] that counts the number of proposalsmade by man m.

也可以基于链表实现，删除头节点即可

Women rejecting/accepting：

• For each woman, create inverse of preference list of men.
• Constant time access for each query after O(n) preprocessing.

Other Understanding

1. 对于解不唯一的样例，Gale-Shapley 算法总会给出相同的匹配吗？

• valid partner: Man m is a valid partner of woman w if there exists some stablematching in which they are matched.
• Man-optimal assignment: Each man receives best valid partner.

All executions of GS yield man-optimal assignment, which is a stable matching.

主动方占优，该算法男性主动发出匹配请求。

Man Optimality

Claim. _GS matching S is man-optimal._*

Pf. (by contradiction)

1. (S* ) Suppose some man is paired with someone other than bestpartner. Men propose in decreasing order of preference  someman is rejected by valid partner.
2. (S* ) Let Y be first such man, and let A be first valid woman that rejects him.
3. Let S be a stable matching where A and Y are matched.
4. (S* ) When Y is rejected, A forms (or reaffirms) engagement with a man, say Z, whom she prefers to Y.
5. Let B be Z's partner in S.
6. (S* ) Z not rejected by any valid partner at the point when Y is rejected by A. Thus, Z prefers A to B. (2,4)
7. (S* ) But A prefers Z to Y. (4)
8. Thus A-Z is unstable in S.

Woman Pessimality

• Woman-pessimal assignment. Each woman receives worst valid partner.

Claim. GS finds woman-pessimal stable matching S*

Pf.

1. Suppose A-Z matched in S*, but Z is not worst valid partner for A.
2. There exists stable matching S in which A is paired with a man, sayY, whom she likes less than Z.
3. Let B be Z's partner in S.
4. Z prefers A to B (in S*. A and B are both valid partners). [man-optimality]
5. Thus, A-Z is an unstable in S

END