Greedy Algorithm
Interval Scheduling
- Job j starts at $s_j$ and finishes at $f_j$.
- Two jobs compatible if they don't overlap.
- Goal: find maximum subset of mutually compatible jobs.
Greedy algorithm.
Consider jobs in increasing order of finish time.Take each job provided it's compatible with the ones already taken.
按照结束时间升序排列: 先完成 DDL 早的
$$\text{Sort jobs by finish times so that }f_1 < f_2 < ... < f_n.\A \leftarrow \emptyset\for, j = 1\text{to n} { \qquad if (job j compatible with A)\qquad A \leftarrow A \cup {j}}\return A $$
Implementation. $O(n log n)$.
- Remember job j* that was added last to A.
- Job j is compatible with A if $s_j < f_{j^*}$.
Analysis:
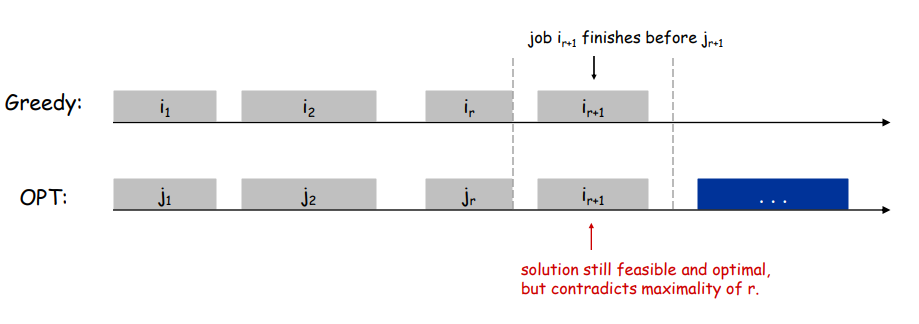
Theorem. Greedy algorithm is optimal.
Pf. (by contradiction)
Assume greedy is not optimal, and let's see what happens.
Let $i_1, i_2, ... i_k$ denote set of jobs selected by greedy.
Let $j_1, j_2, ... j_m$ denote set of jobs in the optimal solution with $i_1 = j_1, i_2 = j_2, ..., i_r = j_r$ for the largest possible value of r.
Interval Partitioning
- Lecture j starts at $s_j$ and finishes at $f_j$.
- Goal: find minimum number of classrooms to schedule all lectures so that no two occur at the same time in the same room.
Def. The depth of a set of open intervals is the maximum number that contain any given time.
同一时间发生任务的最大数量是需要的教室数量的上限
Greedy algorithm:
Consider lectures in increasing order of start time: assign lecture to any compatible classroom
按照开始时间升序排列
$$\text{Sort intervals by starting time so that} s1 < s2 < ... < sn.\d \leftarrow 0\for, j = 1, to, n, {\qquad \text{if (lecture j is compatible with some classroom k)}\qquad \qquad \text{schedule lecture j in classroom k}\qquad else\qquad \qquad \text{allocate a new classroom d + 1}\qquad \qquad \text{schedule lecture j in classroom d + 1}\qquad \qquad d \leftarrow d + 1} $$
Implementation. $O(n log n)$.
- For each classroom k, maintain the finish time of the last job added.
- Keep the classrooms in a priority queue.
Analysis:
Greedy algorithm never schedules two incompatible lectures in the same classroom.
**Theorem. Greedy algorithm is optimal.**Pf.
- Let d = number of classrooms that the greedy algorithm allocates.
- Classroom d is opened because we needed to schedule a job, say j, that is incompatible with all d-1 other classrooms.
- These d jobs each end after $s_j$.
- Since we sorted by start time, all these incompatibilities are caused by lectures that start no later than $s_j$.
- Thus, we have d lectures overlapping at time $s_j$.
- Key observation => all schedules use >= d classrooms. ▪
Scheduling to Minimize Lateness
前面描述的是如何合理安排好任务,这里主要关注,在不可避免会拖延的时候,如何减少拖延损失。
- Single resource processes one job at a time.
- Job j requires $t_j$ units of processing time and is due at time $d_j$.
- If j starts at time $s_j$, it finishes at time $f_j= s_j + t_j$.
- Lateness: $l_j = max{0, fj - dj}$.
- Goal: schedule all jobs to minimize maximum lateness $L = max, l_j$.
Greedy Algorithms:Earliest deadline first. 仍然是按照 DDL 先后排序
$$\text{Sort n jobs by deadline so that} d_1 < d2 < … < d_n\t \leftarrow 0\for, j = 1, to, n\qquad \text{Assign job j to interval} [t, t + t_j]\qquad s_j \leftarrow t, f_j \leftarrow t + t_j\qquad t \leftarrow t + t_j\text{output intervals} [s_j, f_j]$$
Observation. There exists an optimal schedule with no idle time.
Observation. The greedy schedule has no idle time.
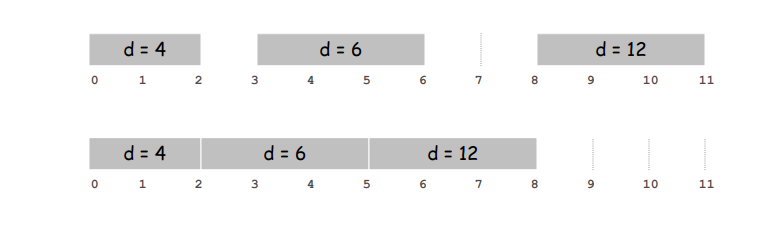
由于贪心算法尽可能直接完成任务,因此没有的间隙 (在不限制开始时间的情况下)
Def.
Inversion: Given a schedule S, an inversion is a pair of jobs i and j such that: i < j but j scheduled before i.
Observation. Greedy schedule has no inversions.Observation. If a schedule (with no idle time) has an inversion, it has one with a pair of inverted jobs scheduled consecutively.
已经按照结束时间排序了,因此贪心算法不会出现 Inversion
Claim. Swapping two consecutive, inverted jobs reduces the number of inversions by one and does not increase the max lateness
Pf. Let $l$ be the lateness before the swap, and let $l'$ be it afterwards.
- $l'_k = l_k$ for all $k \neq i, j$
- $l'_i \leq l_i$
- If job j is late:
Optimal Caching
Caching.
- Cache with capacity to store k items.
- Sequence of m item requests $d_1, d_2, …, d_m$.
- Cache hit: item already in cache when requested.
- Cache miss: item not already in cache when requested: must bring requested item into cache, and evict some existing item, if full.
Goal. Eviction schedule that minimizes number of cache misses.
Farthest-in-future: Evict item in the cache that is not requested until farthest in the future
Theorem. [Bellady, 1960s] FF is optimal eviction schedule.Pf. Algorithm and theorem are intuitive; proof is subtle.
Def. A reduced schedule is a schedule that only inserts an item intothe cache in a step in which that item is requested.
Intuition. Can transform an unreduced schedule into a reduced onewith no more cache misses.
Claim. Given any unreduced schedule S, can transform it into a reducedschedule S' with no more cache misses.
Pf. (by induction on number of unreduced items)
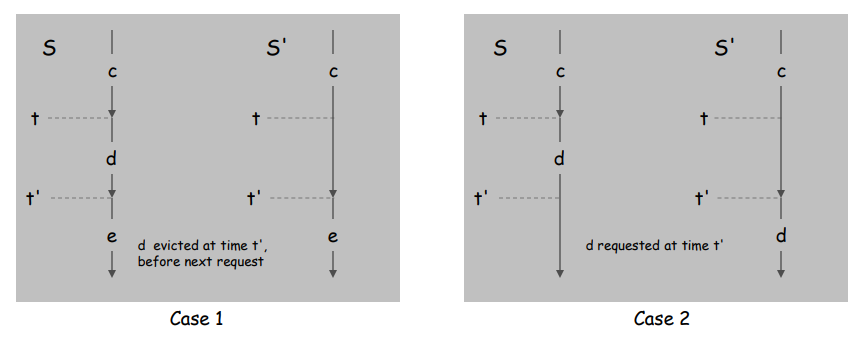
Suppose S brings d into the cache at time t, without a request.
Let c be the item S evicts when i t brings d into the cache.
- Case 1: d evicted at time t', before next request for d.
- Case 2: d requested at time t' before d is evicted. ▪
Theorem. FF is optimal eviction algorithm
Pf: // TODO: p30 greedy
Shortest Paths in a Graph
略
Minimum Spanning Tree
Given a connected graph G = (V, E) with real-valued edge weights $c_e$, an MST is a subset of the edges T E such that T is a spanning tree whose sum of edge weights is minimized.
本质是寻找权重最小且能使这个图保持连通性的 n-1 条边
Kruskal's algorithm.
Start with $T = \emptyset $. Consider edges in ascending order of cost.
Insert edge e in T unless doing so would create a cycle.

Implementation. Use the union-find data structure.
- Build set T of edges in the MST.
- Maintain set for each connected component.
- O(m log n) for sorting and O(m (m, n)) for union-find.
Reverse-Delete algorithm.
Start with T = E. Consider edges in descending order of cost.
Delete edge e from T unless doing so would disconnect T.
Prim's algorithm
Start with some root node s and greedily grow a tree T from s outward.
At each step, add the cheapest edge e to T that has exactly one endpoint in T.

Implementation. Use a priority queue ala Dijkstra.
- Maintain set of explored nodes S.
- For each unexplored node v, maintain attachment cost a[v] = cost of cheapest edge v to a node in S.
- O(n2) with an array; O(m log n) with a binary heap.
Def:
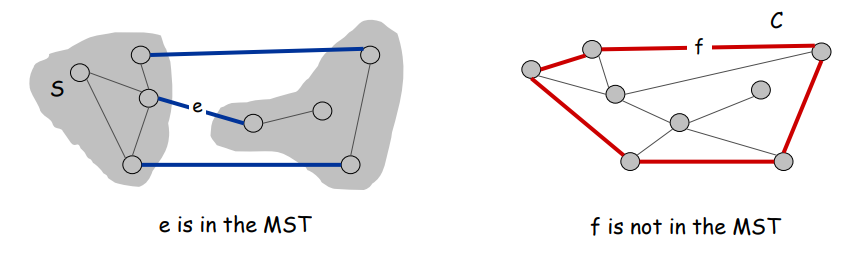
Cut property:
Let S be any subset of nodes, and let e be the min cost edge with exactly one endpoint in S. Then the MST contains e.
Cycle property:
Let C be any cycle, and let f be the max cost edge belonging to C. Then the MST does not contain f.
Cycle
Set of edges the form a-b, b-c, c-d, …, y-z, z-a.
Cutset
A cut S is a subset of nodes. The corresponding cutset D is the subset of edges with exactly one endpoint in S

Claim. A cycle and a cutset intersect in an even number of edges.
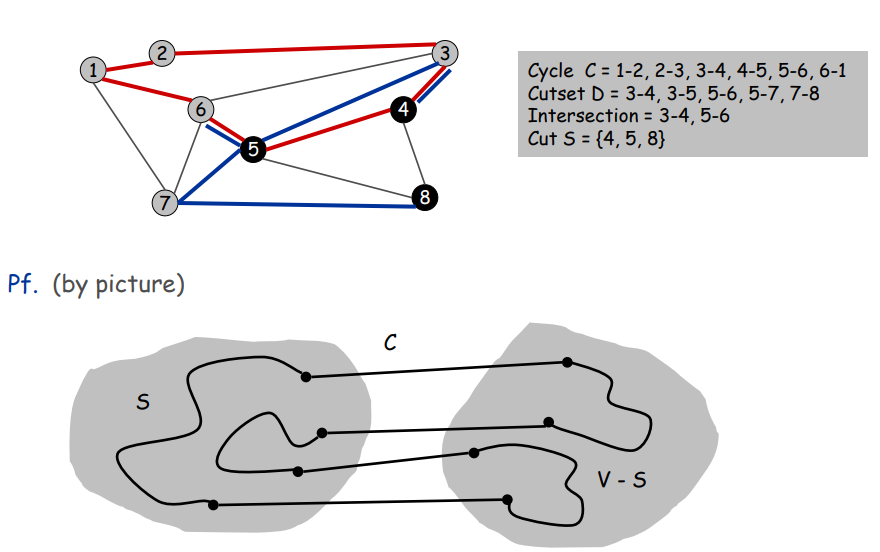
证明:略 p10 MST
优化
Kruskal 和 Prim 都只能计算权重不同的情况,若存在权重相同的边,则在比较阶段优化即可:

Clustering
聚类的本质和最小生成树差不多,无非是最小生成树是一个类,需要 n-1 条边
对于聚类数k,需要 n-k 条边,及在最小生成树的基础上删去 (k-1) 条权重最高的边即可
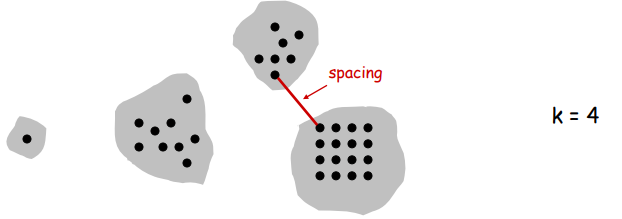
k-clustering: Divide objects into k non-empty groups.
Distance function: Assume it satisfies several natural properties.
- $d(p_i, p_j) = 0$ iff $p_i = p_j$ (identity of indiscernibles)
- $d(p_i, p_j) \geq 0$ (nonnegativity)
- $d(p_i, p_j) = d(p_j, p_i)$ (symmetry)
Spacing: Min distance between any pair of points in different clusters.
Clustering of maximum spacing: Given an integer k, find a k-clustering of maximum spacing.
Single-link k-clustering algorithm
Form a graph on the vertex set U, corresponding to n clusters.
Find the closest pair of objects such that each object is in a different cluster, and add an edge between them to merge these two clusters into a new cluster.
Repeat n-k times until there are exactly k clusters.
Key observation. This procedure is precisely Kruskal's algorithm (except we stop when there are k connected components).
Remark. Equivalent to finding an MST and deleting the k-1 most expensive edges.
证明:反证法
Huffman Codes
省略了证明部分

T(n) = T(n-1) + O(n)
so time complexity is $O(N^2)$
Using priority queue: $T(n) = T(n-1) + O(logn) => O(NlogN)$
Claim. Huffman code for S achieves the minimum ABL of any prefix code.
**Pf. (by induction)**Base: For n=2 there is no shorter code than root and two leaves.Hypothesis: Suppose Huffman tree T’ for S’ with $\omega$ instead of y and z is optimal. (IH)Step: (by contradiction)
- Suppose Huffman tree T for S is not optimal.
- So there is some tree Z such that ABL(Z) < ABL(T).
- Then there is also a tree Z for which leaves y and z exist that aresiblings and have the lowest frequency (see observation).
- Let Z’ be Z with y and z deleted, and their former parent labeled $\omega $.
- Similar T’ is derived from S’ in our algorithm.
- We know that $ABL(Z’)=ABL(Z)-f_\omega$, as well as $ABL(T’)=ABL(T)-f_\omega$.
- But also ABL(Z) < ABL(T), so ABL(Z’) < ABL(T’).
- Contradiction with IH.