Graph

Basic Definitions and Applications

Undirected Graphs

Undirected graph. G = (V, E)

• V = nodes.
• E = edges between pairs of nodes.
• Captures pairwise relationship between objects.
• Graph size parameters: n = |V|, m = |E|.

Directed Graphs

Graph Representation

Adjacency matrix - 邻接矩阵

n-by-n matrix with $A_{uv} = 1$ if (u, v) is an edge.

• Two representations of each edge.
• Space proportional to $n^2$.
• Checking if (u, v) is an edge takes $\Theta(1)$ time.
• Identifying all edges takes $\Theta(n^2)$ time

Adjacency List - 邻接表

Adjacency list. Node indexed array of lists.

• Two representations of each edge.
• Space proportional to m + n.
• Checking if (u, v) is an edge takes $O(deg(u))$ time.
• Identifying all edges takes $\Theta(m + n)$ time

离散数学中图论部分补充的 关联矩阵

Definition

Paths and Connectivity

Path:

A path in an undirected graph G = (V, E) is a sequence P of nodes $v_1, v_2, …, v_{k-1}, v_k$ with the property that each consecutive pair $v_i, v_{i+1}$ is joined by an edge in E.

simple path:

A path is simple if all nodes are distinct.

没有回路，每个顶点只经过一次

connected：

An undirected graph is connected if for every pair of nodes u and v, there is a path between u and v.

Cycles:

A cycle is a path $v_1, v_2, …, v_{k-1}, v_k$ in which $v_1 = v_k, k > 2$, and thef irst k-1 nodes are all distinct.

Tree

An undirected graph is a tree if it is connected and does not contain a cycle.

Theorem. Let G be an undirected graph on n nodes. Any two of the following statements imply the third.

• G is connected.
• G does not contain a cycle.
• G has n-1 edges.

Rooted tree:

Given a tree T, choose a root node r and orient each edge away from r.

Algorithm

Connectivity in Undirected Graph

• s-t connectivity problem

Given two node s and t, is there a path between s and t?

• s-t shortest path problem

Given two node s and t, what is the length of the shortest path between s and t?

Connectivity in Directed Graphs

• Directed reachability

Given a node s, find all nodes reachable from s

• Directed s-t shortest path problem

Given two node s and t, what is the length of the shortest path between s and t?

• Graph search

BFS extends naturally to directed graphs.

Strong Connectivity

• mutually reachable:

Node u and v are mutually reachable if there is a path from u to v and also a path from v to u.

• strongly connected :

A graph is strongly connected if every pair of nodes is mutually reachable.

Lemma. Let s be any node. G is strongly connected iff every node is reachable from s, and s is reachable from every node

• Pf. Follows from definition.
• Pf. Path from u to v: concatenate u-s path with s-v path.Path from v to u: concatenate v-s path with s-u path.

Topological Ordering

• Def. A topological order of a directed graph G = (V, E) is an ordering of its nodes as $v_1, v_2, …, v_n$so that for every edge $(v_i, v_j)$ we have i < j.
• Lemma. If G has a topological order, then G is a DAG.

DAGs (Directed Acyclic Graphs) 有向无环图

Def. An DAG is a directed graph that contains no directed cycles

Ex. Precedence constraints: edge $(v_i, v_j)$ means $v_i$ must precede $v_j$.

Lemma. If G has a topological order, then G is a DAG.

Pf. (by contradiction)

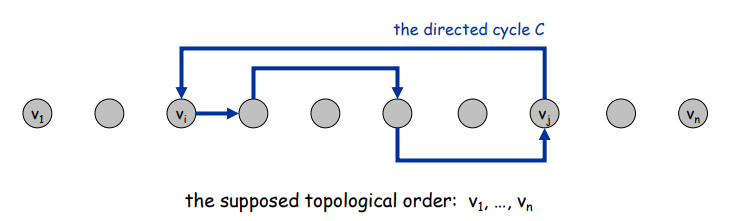
• Suppose that G has a topological order $v_1, …, v_n$ and that G also has a directed cycle C. Let's see what happens.
• Let $v_i$ be the lowest-indexed node in C, and let $v_j$ be the node just before $v_i$; thus $(v_j, v_i)$ is an edge.
• By our choice of i, we have i < j.
• On the other hand, since $(v_j, v_i)$ is an edge and $v_1, …, v_n$is a topological order, we must have j < i, a contradiction.

Lemma. If G is a DAG, then G has a node with no incoming edges.

Pf. (by contradiction)

• Suppose that G is a DAG and every node has at least one incomingedge. Let's see what happens.
• Pick any node v, and begin following edges backward from v. Since vhas at least one incoming edge (u, v) we can walk backward to u.
• Then, since u has at least one incoming edge (x, u), we can walkbackward to x.
• Repeat until we visit a node, say w, twice.
• Let C denote the sequence of nodes encountered between successive visits to w. C is a cycle.

Lemma. If G is a DAG, then G has a topological ordering.

Pf. (by induction on n)

• Base case: true if n = 1.
• Given DAG on n > 1 nodes, find a node v with no incoming edges.
• G - { v } is a DAG, since deleting v cannot create cycles.
• By inductive hypothesis, G - { v } has a topological ordering.
• Place v first in topological ordering; then append nodes of G - { v } in topological order. This is valid since v has no incoming edges. ▪

不断地添加入度为0的节点并删除即可

Breadth First Search

Theorem: For each i, $L_i$ consists of all nodes at distance exactly i from s. There is a path from s to t iff t appears in some layer

Property. Let T be a BFS tree of G = (V, E), and let (x, y) be an edge of G. Then the level of x and y differ by at most 1.

L0 = {s}.
L1 = all neighbors of L0
L2 = all nodes that do not belong to L0 or L1, and that have an edge to a node in L1
Li+1 = all nodes that do not belong to an earlier layer, and that have an edge to a node in Li

Analysis:

• The above implementation of BFS runs in $O(m + n)$ time if the graph is given by its adjacency representation.

Pf.

Easy to prove O(n2) running time:

• at most n lists L[i]
• each node occurs on at most one list; for loop runs  n times
• when we consider node u, there are <= n incident edges (u, v), and we spend O(1) processing each edge

Actually runs in O(m + n) time:

• when we consider node u, there are deg(u) incident edges (u, v)
• total time processing edges is $\sum_{u∈V}deg(u) = 2m$

Connected Component

Find all nodes reachable from s.

R will consist of nodes to which S has a path
Initially R = {s}
While there is an edge (u, v) where u∈R and v∉R
	Add v to R
Endwhile

Theorem. Upon termination, R is the connected component containing s.

• BFS = explore in order of distance from s.
• DFS = explore in a different way

无向图的联通分量及并查集，

有向图的强连通分量需要更多的算法思考

包括图的翻转等，可以参考 DSAA

Bipartite Graphs

Def: An undirected graph G = (V, E) is bipartite if the nodes can be colored red or blue such that every edge has one red and one blue end.

二分图，可以使用两种颜色完成染色，匹配问题

Applications:

• Stable marriage: men = red, women = blue.
• Scheduling: machines = red, jobs = blue.

Benefits:

If a giving graph is bipartite, then Many graph problems become

• easier if the underlying graph is bipartite (matching)
• tractable if the underlying graph is bipartite (independent set)

Lemma. If a graph G is bipartite, it cannot contain an odd length cycle.

Pf. Not possible to 2-color the odd cycle, let alone G.

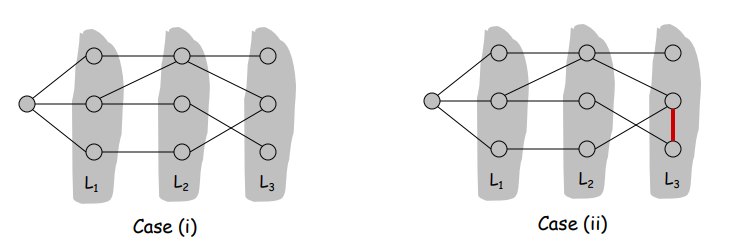
Lemma. Let G be a connected graph, and let $L_0, …, L_k$ be the layersproduced by BFS starting at node s. Exactly one of the following holds.

• (i) No edge of G joins two nodes of the same layer, and G is bipartite.
• (ii) An edge of G joins two nodes of the same layer, and G contains an odd-length cycle (and hence is not bipartite).

使用 BFS 检测二分，可结合下图理解

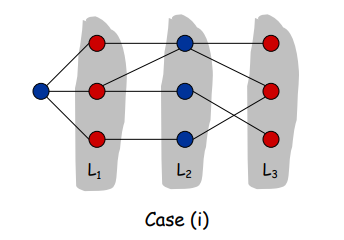
Pf. (1)

• Suppose no edge joins two nodes on same layer.
• By previous property on page 19, this implies every edge join two nodes in adjacent layers.
• Give nodes on odd levels = red, nodes on even levels = blue -> Bipartition.

Pf. (ii)

Suppose (x, y) is an edge with x, y in same level $L_j$.

Let $z = lca(x, y)$ = lowest common ancestor.

Let Li be level containing z.

Consider cycle that takes edge from x to y, then path from y to z, then path from z to x.

Its length is 1 + (j-i) + (j-i), which is odd.

​ (x, y) y->z z->x

Corollary. A graph G is bipartite iff it contain no odd length cycle.

Strong Connectivity

Theorem: Can determine if G is strongly connected in $O(m + n)$ time.

Pf.

• Pick any node s.
• Run BFS from s in G. ($O(m+n)$)
• Run BFS from s in $G^{rev}$. (s->v $G^{rev}$ become v->s in G)
• Return true iff all nodes reached in both BFS executions.
• Correctness follows immediately from previous lemma.

Tpological ordering.

不断地添加入度为0的节点，并从图中删除该节点及与它相连的边即可

The algorithm finds a topological order in $O(m + n)$ time.

Pf.

• Maintain the following information:
• count[w] = remaining number of incoming edges
• S = set of remaining nodes with no incoming edges
• Initialization: O(m + n) via single scan through graph.
• Update: to delete v
• remove v from S
• decrement count[w] for all edges from v to w, and add w to S if count[w] hits 0
• this is O(1) per edge ▪

Dijkstra's Shortest Path Algorithm

略

每次添加 能够到已经遍历过节点的最近节点即可